Facebook の機械学習ライブラリをためすチュートリアルの第２回です。前回のエントリでインストールした、Facebook の時系列分析用ライブラリ Prophet 。今回は公式のガイドにそって実際に分析をしてみます。
** Sorry, this note is Japanese only, but please take a look at some code snippets. Hope it helps you.
参考：Quick Start - Prophet（公式のチュートリアル、英語です）
インストールまだの人はこちらからお先にどうぞ。
Facebook の機械学習 ライブラリ Prophet - Quick Start の内容
公式ドキュメントにはこのライブラリの使い方がかなり詳しく説明されていますが、一番初めに挑む Quick Start は、前回のインストール記事の中でも参照した参考ブログで紹介されていた、Payton Mannings というアメフト選手の Wikipedia ページのページビューを予測する、という
内容です。
データ サイエンティストでも機械学習の専門でもない素人ですが、Facebook の公式ドキュメントをトレースするだけでそれらしいことはできました。
英語ではありますが、最近賢くなった Google 先生の翻訳に頼りながら読んでもわかるぐらい丁寧な説明がされてて、この記事は雑な翻訳ぐらいの意味しかない・・・(; ;) のですが、最後に少し補足を足しつつ、メモとして残しておきたいと思います。
サンプルデータの読み込み
まず、必要なモジュールの import から。
import pandas as pd import numpy as np from fbprophet import Prophet
そして次に、今回分析に用いる Payton Mannings さんの Wikipedia ページのデータですが、Prophet の github リポジトリの中にもCSVファイルとして置いてくれています（ココ）。
このファイルを pandas の read_csv メソッドで読み込んで pandas の DataFrame オブジェクトにします。
df = pd.read_csv('https://raw.githubusercontent.com/facebookincubator/prophet/master/examples/example_wp_peyton_manning.csv') df['y'] = np.log(df['y']) df.head()
ds というのがタイムスタンプ（このデータでは日次になってます）で、y が予測したい目的変数です（今回は、ページビュー）。
２行目では元の目的変数ではなく、対数を取ってあらためてそれを目的変数にセットしています。あとで触れますが、恐らくこれはナマのページビューを扱うと極端にページビューが大きい日があったりして予測精度が低くなるのを防ぐための工夫かと思われます。
実際のデータは df.head() の通りです。
| ds | y | |
|---|---|---|
| 0 | 2007-12-10 | 9.590761 |
| 1 | 2007-12-11 | 8.519590 |
| 2 | 2007-12-12 | 8.183677 |
| 3 | 2007-12-13 | 8.072467 |
| 4 | 2007-12-14 | 7.893572 |
モデルの学習 〜 将来データの予測まで
Prophet は、最早 Python のデータ分析・機械学習ライブラリの標準となりつつある、scikit-learn に似たインターフェースとなるように意識されているようで、モデルのインスタンスを生成したあと、fit というメソッドで学習し、predict というメソッドで学習済みのモデルを用いて将来の予測を行います。
まず、モデルの生成と学習がこんな感じ。
m = Prophet() m.fit(df)
そして、将来データの予測ですが、先に予測する期間を定義した dataframe を make_future_dataframe というメソッドを用いて作成します。
future = m.make_future_dataframe(periods=365)
future.tail()
make_future_dataframe の引数 periods は予測をする期間です（ここでは 365 日分予測しようとしている）。
future.tail() の結果でわかるように、生成された dataframe future は、今のところ予測すべき期間の日付が ds 列に格納されています。
| ds | |
|---|---|
| 3265 | 2017-01-15 |
| 3266 | 2017-01-16 |
| 3267 | 2017-01-17 |
| 3268 | 2017-01-18 |
| 3269 | 2017-01-19 |
で、このあと predict メソッドを実行すると、この future に対応する予測データが得られる、という具合です。
forecast = m.predict(future)
m.predict の戻り値 forecast は dataframe で、次のようなデータ項目を含んでいます。
>>> forecast.columns Index(['ds', 't', 'trend', 'seasonal_lower', 'seasonal_upper', 'trend_lower', 'trend_upper', 'yhat_lower', 'yhat_upper', 'weekly', 'weekly_lower', 'weekly_upper', 'yearly', 'yearly_lower', 'yearly_upper', 'seasonal', 'yhat'], dtype='object')
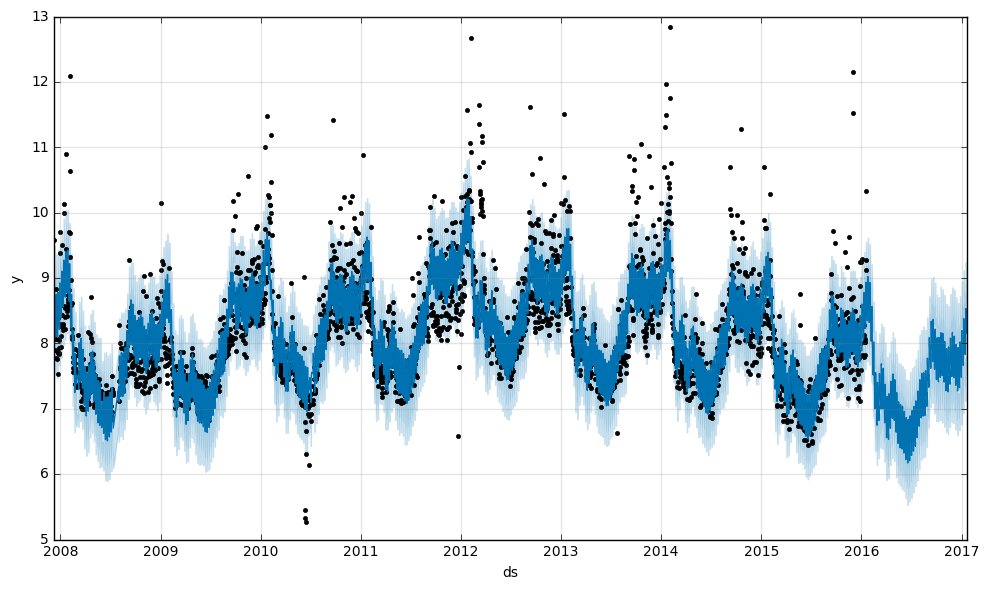
そして、この中の yhat というのがページビュー（対数）の予測値です。便利なことに plot というメソッドでこの予測値とその分散の幅をグラフで表示してくれます。
m.plot(forecast)
これが冒頭の画像です（再掲）。
黒い点が実際に観測されたページビュー（対数）で、青い線が学習によって得られたモデル値、薄水色の幅は分散のようです。よく見ると2017年以降の部分には黒い点がなく、予測データであることがわかります。
予測データ forecast に含まれるその他の項目は様々な粒度での予測データのようです。yearly、weekly、trend に関しては、plot_components というメソッドでグラフを書いてくれます。
m.plot_components(forecast)
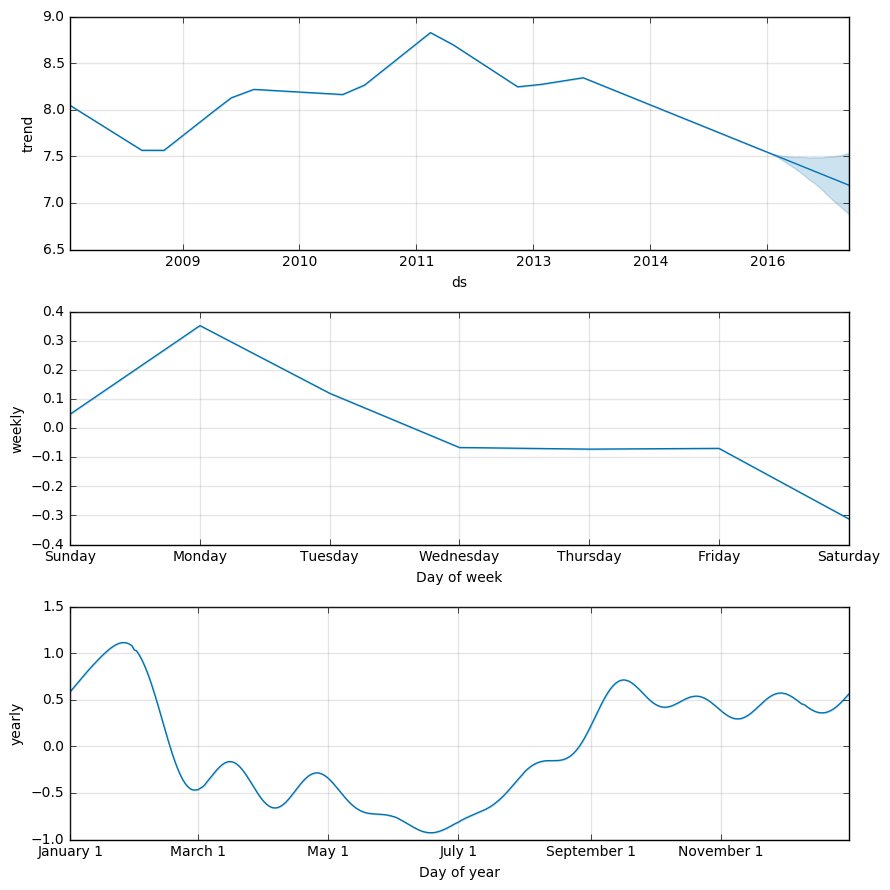これを見ると、
- 2008年と2011年の前半に大きなトレンドの変化が発生している
- 曜日の傾向としては、日曜日・月曜日はアクセスが増えやすく、以降の曜日は下降傾向
- 年間の傾向としては、7月すぎたあたりからアクセスが増え始め、9-12月は高い位置で推移、1月終わり ~ 2月ごろにピークを迎える
というようなことが読み取れます。
予測の精度について
ここまでの内容を見ていると、カンタンにそれらしい結果が得られているようでイイ感じなのですが、一つ疑問がでてきます。
「カンタン・それらしいのはいいけど、どの程度の精度で予測できているの・・・？」
そこで、これまた雑ではありますが、
- 実際に観測値が存在する期間を予測し、モデルによる予測値と比較する
という、簡易的な方法で予測精度を調べてみました。
予測値と観測値の比較を評価する指標には scikit-learn の MSE を使いました。例えば、2008年のデータを使って学習し、2009年のデータで精度を評価する場合、こんな感じです。
df['ts'] = pd.to_datetime(df['ds']) df2008 = df[df.ts >= pd.to_datetime('2008-01-01')][df.ts <= pd.to_datetime('2008-12-31')] df2009 = df[df.ts >= pd.to_datetime('2009-01-01')][df.ts <= pd.to_datetime('2009-12-31')] m = Prophet() m.fit(df2008) future = m.make_future_dataframe(periods=365) forecast = m.predict(future) y_pred = forecast.yhat.values y_true = df2009.y.values from sklearn.metrics import mean_squared_error mse = mean_squared_error(y_pred, y_true)
こんな感じのコードですが、実際には観測データには欠損などがあり、df2009.y と forecast.yhat はデータの件数が異なります。なので、
- ts をキーにして df2009 を forecast をマージした上で
- 観測データの欠損値を補完（今回は平均値で補完しました）
という具合にデータを整備してから MSE を計算してます。
その結果はどうだったのか？というと、
>>> print(mse) 0.69910605467382758
・・・
・・・あれ・・・？なんか意外と精度低い？？（ MSE って誤差のことだから数字が小さい方がいいよね・・・？？）
グラフ上で forecast の上に観測値をのせてみるとこんな感じです。
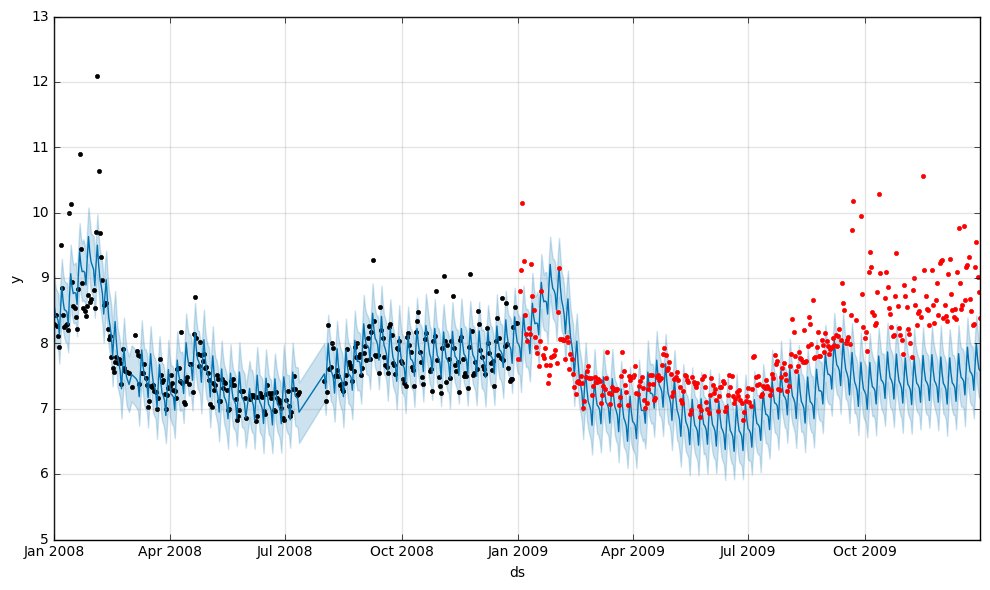
ブルーのラインが予測、黒い点は学習に使われている期間の観測値で、赤い点が予測期間の観測値です。
確かに、予測のラインとややずれてるのと、年後半は大きくトレンドも外している感じがしますね。
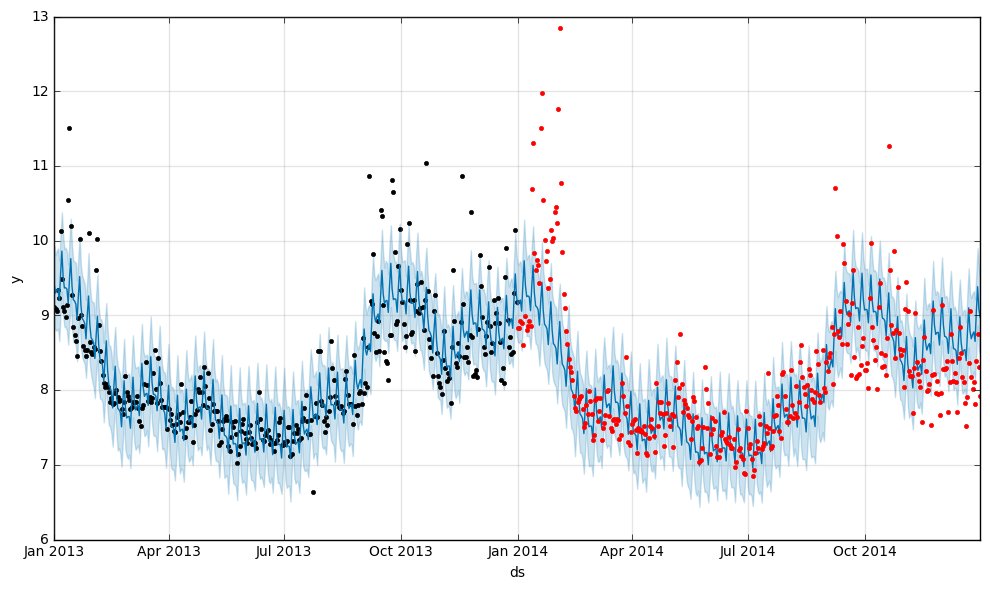
たまたまこの年だけって可能性もあるので、試しに 2013年（学習）-> 2014年（予測）でやってみるとやはり改善しました。
>>> print(mse) 0.3903252278029366
グラフ上にプロットしてみても2008年 -> 2009年の時よりうまく予測できてる感じです。
学習データの年次によってこんなに精度が違うのはちょっと困りますね。そこで、予測したい期間に対してどの程度の期間分学習データを取れば良いのか調べてみました。
やり方は、
- 予測したい期間からT周期分遡った期間を学習データとし MSE を計算
- T に対する MSE の推移をプロットする
というカンタンなものです。今の場合、予測したい期間は１年です。今回のデータで一番あたらしい１年分というと2015年なので、2015年分を予測するために、2015/1/1から 0.5年分 -> 1.0年分 -> 1.5年分・・・という具体に過去に遡って学習させました。
0.5年分ずつ期間を伸ばしたのは、１年の周期性があるなら、予測期間の整数倍を学習データとするか半整数倍とするかで何らかの違いがでるかも？と思ったからです。
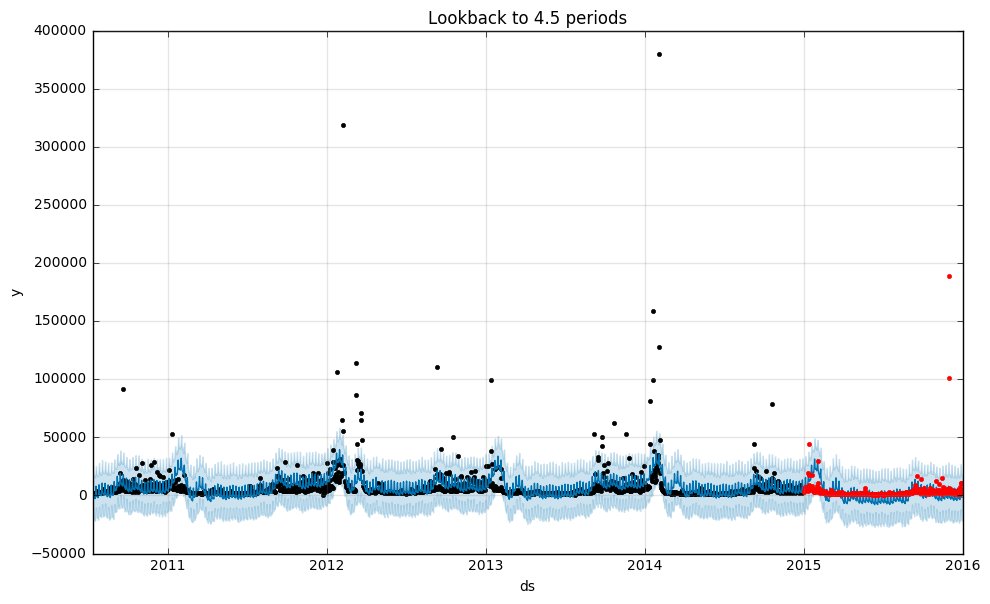
結果はこのようになりました。
グラフの一番左は学習データ＝0.5年分で、ズバ抜けて成績が悪いですね・・・実際の予測状況はこうです。
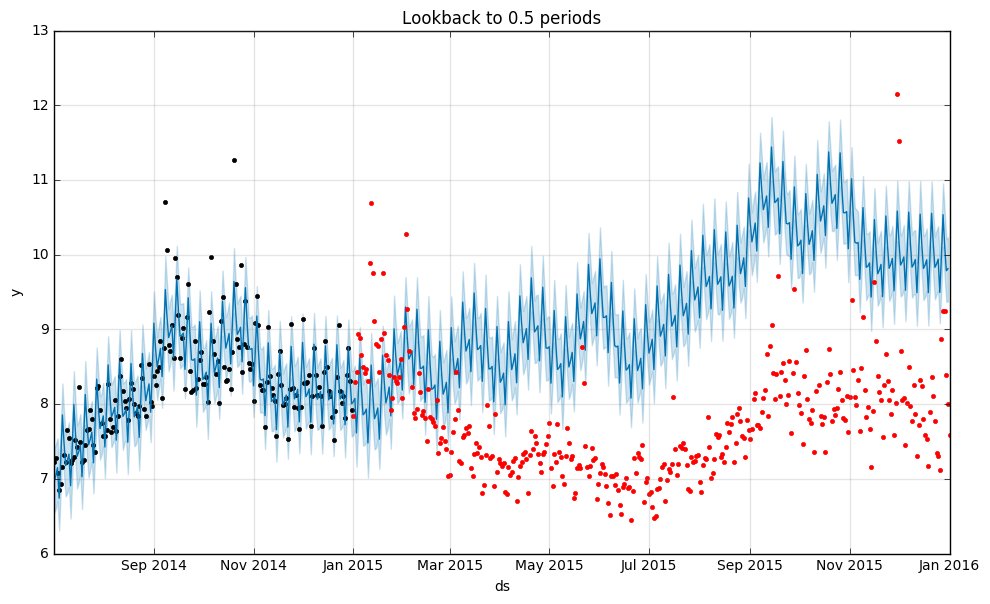
あたりまえっちゃあたりまえですが、やはり1年分の予測をするにあたり半年分では学習データが足りないようです。
更に、その他の違いがわかりにくいので0.5年分のをはずしてみました。
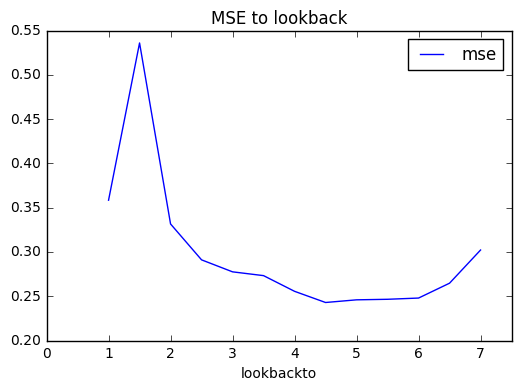
だいたい学習期間が長いほうが精度が高いことが読み取れるのですが、面白いのが、
- 1.5年分学習するよりは、1年分で学習したほうがはるかに制度が高い
- 精度は4.5年分のところで底打ちし、6.5周期目あたりから MSE が高くなってきている
という点です。前者はなんとなく予想した通りで、中途半端に0.5周期分学習データを増やすぐらいなら、キッチリ1周期分のほうが良いようです。
実際の予測と観測データはこんな具合です（上が1年分、下が1年半分で学習したもの）。
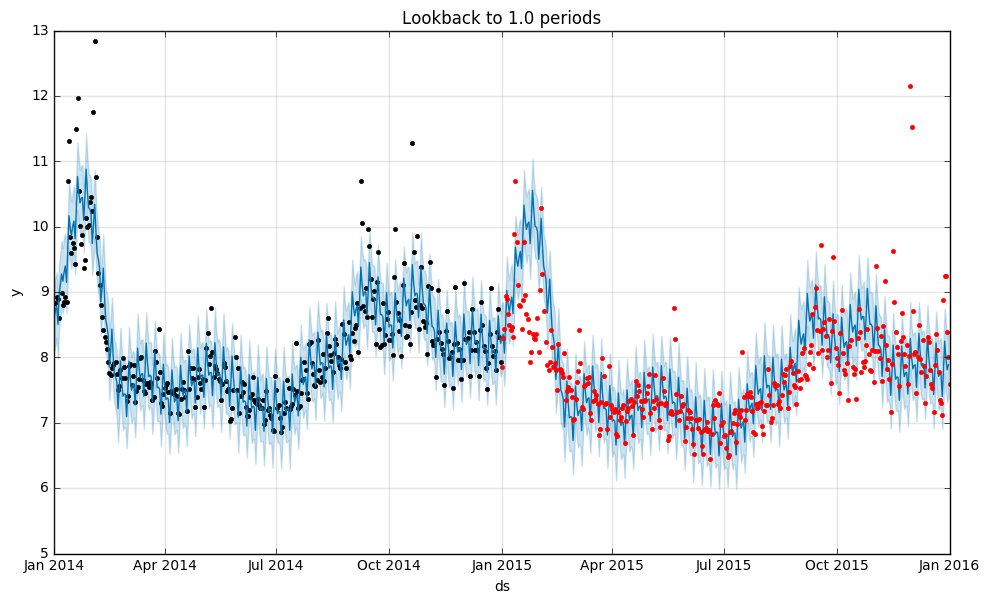
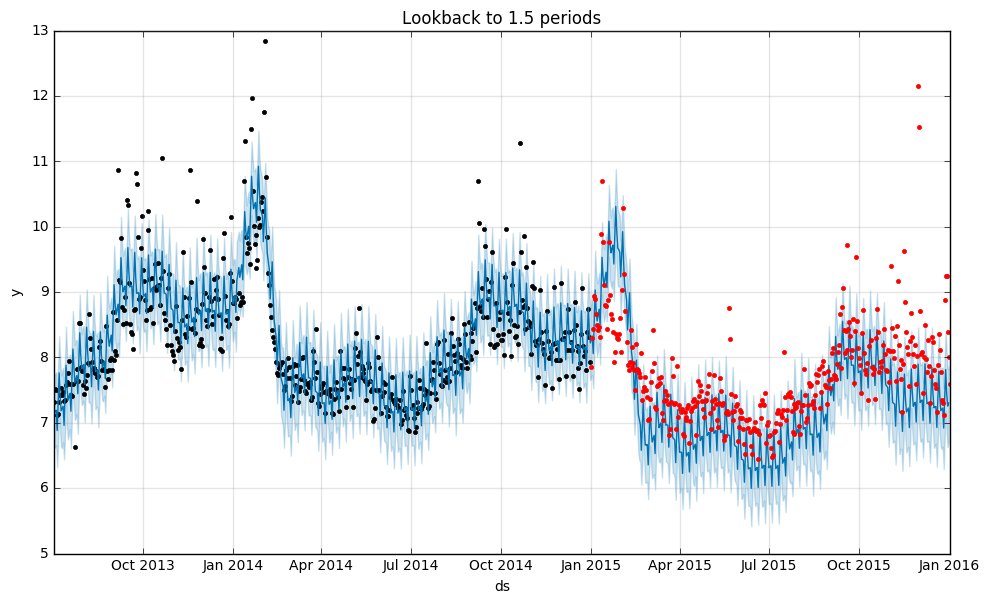
1.5年分学習した方（下）が、予測がやや実際の観測データの中心をはずしているようですね。
また、後者はハッキリと理由はわからないのですが、2015年から4期前というと2011年ということになるのでちょうどトレンドの変化があったころです。つまり、異なるトレンドの期間が学習データに加わることで予測の精度が落ちてきている、という感じがしますね。
ほんとうはクロスバリデーションしたり、とモデルの精度はもっと緻密に調べる必要があるでしょうし、雑な分析なのでこの見解が合ってるのかイマイチ自身はないですが、どの程度の期間を学習データとするのか？といったあたりがチューニングすべきパラメータになってくるのかもしれません。
補足
記事の冒頭で書きましたが、ページビューそのものではなく、対数を取っていることについて確認するために対数ではない元々の値でも試してみました。
すると、グラフと MSE の値はこんな感じ。
>>> print(mse) 161616544.708
やはり、今回のデータは外れ値の影響が大きいから対数を取るんですね。勉強になります。
この記事には全然関係ないのですが、naoya さん（id:naoya）っていう方がこの記事をはてブしてくれていて、プロフィール拝見したら元中の人だしめっちゃ偉い人っぽかったのに、わたしはそれをまるっきり無視してて穴に入りたくなりました。
いまさらですが、この場を借りてお礼を・・・こんなわたしの記事を読んでいただいてありがとうございました。
機械学習 ・ 人工知能 関連の他の記事
datalove.hatenadiary.jp datalove.hatenadiary.jp datalove.hatenadiary.jp datalove.hatenadiary.jp